SV随机化控制

发表于 分类于 ，
System Verilog CRT控制方法，以及随机化函数

控制方法

分布控制

  • 系统预定义的回调函数，可以在类中重写，以便在随机化过程的关键节点注入自定义逻辑
    • pre_randomize()：在开始执行、求解约束之前自动调用
    • post_randomize()：在成功执行、赋值之后自动调用
    • 如果randmoize()失败，post_randomize不会被调用
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Packet;
    rand bit [7:0] length;
    rand bit [7:0] payload[];
    bit [7:0] checksum;

    constraint valid_length {
        length inside { [1:10] };
    }

    // 在随机化前，动态调整payload数组的大小
    function void pre_randomize();
        payload = new[length]; // 根据length的约束值（但尚未随机化）预留空间
        $display("Pre-randomize: Setting payload size to %0d", length);
    endfunction

    // 在随机化后，计算payload的校验和
    function void post_randomize();
        checksum = 0;
        foreach (payload[i]) begin
            checksum += payload[i];
        end
        $display("Post-randomize: Checksum calculated as 0x%h", checksum);
    endfunction
endclass

禁用函数

禁用变量

  • 禁用变量：rand_mode()，临时关闭某个变量的随机化，使其在randomize()调用过程中保持当前值不变
    • rand_mode(0)：关闭指定变量的随机化
    • rand_mode(1)：开启指定变量的随机化
    • rand_mode()：返回变量的当前随机化状态
1
2
3
4
5
6
7
8
9
class Register;
    rand bit [3:0] value;
    rand int test;
endclass

Register r = new;
r.value.rand_mode(0);    // 关闭value的随机化
r.value = 4'b1010; // 手动赋值
r.randomize();     // 调用randomize()后，value的值将保持为4‘b1010不变

禁用约束

  • 禁用约束：constraint_mode()，每个约束块都能被单独开启或关闭
    • constraint_mode(0)：禁用指定的约束
    • constraint_mode(1)：启用指定的约束
    • constraint_mode()：返回当前约束的启用状态
1
2
3
4
5
6
7
8
9
10
11
12
class Bus;
    rand int addr;
    constraint slow_addr { addr inside { [0:100] }; }
    constraint fast_addr { addr inside { [1000:2000] }; }
endclass

Bus b = new;
b.fast_addr.constraint_mode(0); // 禁用fast_addr约束
b.randomize();                  // addr 将在 0-100 内随机
b.slow_addr.constraint_mode(0); // 也禁用slow_addr约束
b.fast_addr.constraint_mode(1); // 启用fast_addr约束
b.randomize();                  // addr 将在 1000-2000 内随机

过程化随机

随机选择

  • randcase
    • 是一个过程化的加权随机选择语句，根据指定权重从多个分支中随机选择一条来执行
    • 不像概率约束中权重分布用于随机化数据值，而是用于随机化控制流
  • 下例为使用randcase和随机化函数$urandom_range的随机控制
1
2
3
4
5
6
7
8
9
initial begin
    bit [15:0] len;
    randcase
        1: len = $urandom_range(0,2); // 10%: 0, 1, 2
        8: len = $urandom_range(3,5); // 80%
        1: len = $urandom_range(6,7); // 10%
    endcase
    $display("len = %0d", len);
end

随机序列

  • randsequence

    • 是一个过程化的随机序列生成语句，可以在执行过程中逐步调试
    • 不像迭代约束中的随机序列只能通过调用randomize()得到随机化结果而无法知道执行过程

  • 两种过程化随机语句的比较

    • randsequence也能像randcase一样实现加权选择，但从代码可读性、编译速度等方面都逊于randcase
    • 反过来看，randsequence生成复杂、有序、多层次的序列是randcase无法做到的
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
task do_something();
    randcase
        70 : generate_normal();    // 70% 概率
        20 : generate_corner();    // 20% 概率
        10 : generate_error();     // 10% 概率
    endcase
endtask

task do_something();               // 用 randsequence 模拟 randcase 的功能
    randsequence ( action )        // 主产生式命名为 'action'
        action : weight(70) : { generate_normal(); }  |
                  weight(20) : { generate_corner(); }  |
                  weight(10) : { generate_error(); }   ;
    endsequence
endtask

randsequence ( test_flow )          // 只能用 randsequence 实现的复杂序列
    test_flow   : setup ( read_operation | write_operation )+ check ; // 序列结构，反映顺序
    setup       : { configure_dut(); } ;
    read_operation  : single_read | burst_read ; // 子选择
        single_read : { do_single_read(); } ;
        burst_read  : { do_burst_read(); } ;
    write_operation : { do_write(); } ;
    check       : { check_results(); } ;
endsequence
  • randsequence语法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
randsequence ( main ) // 从'main'产生式开始
  // 主序列：配置，然后执行一些操作，最后检查
  main : setup ( read_op | write_op )+ check { $display("Done"); } ;

  // 配置产生式
  setup : { $display("Setup Phase"); } 
          { configure(); } ;

  // 带权重的读操作
  read_op : weight(2) : { single_read(); } | 
            weight(1) : { burst_read(); } ;

  // 写操作（可选的调试）
  write_op : { single_write(); } 
             ( { $display("Debug"); } )? ; // 可选调试信息

  // 检查产生式
  check : { verify(); } ;
endsequence
  • 下例为使用randsequence进行递归操作的命令发生器
    • 定义了一个名为stream的随机序列，其产生式定义了三种操作的权重分布
    • 各操作的产生式都包含了两个选项，不指定权重时默认各占50%概率
      • cfg_read操作的第一个选项为执行一次cfg_read_task()后结束
      • 第二个选项为执行一次任务后，递归调用自身cfg_read
      • 因此cfg_read操作至少会执行一次cfg_read_task()，其余两个操作同理
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
initial begin
  for (int i = 0; i < 15; i++) begin
    randsequence (stream)
      stream: cfg_read = 1 |                            // 外部权重
              io_read = 2 |
              mem_read = 5;                             // steam的产生式
      cfg_read: { cfg_read_task(); } |                  // cfg_read的产生式
                  { cfg_read_task(); } cfg_read;          // 权重为50%，递归执行
      io_read: weight(3) : { io_read_task(); } |        // 内部权重，权重为3
                 weight(1) : { io_read_task(); } io_read; // 权重为1，但递归执行
      mem_read: { mem_read_task(); } ;                  // 该操作只执行一次任务
    endsequence
  end
end

task cfg_read_task();
    ...
endtask

...

种子与函数

随机化种子

  • 随机化算法是伪随机的，由一个初始的种子值驱动，相同的种子会产生完全相同的随机数序列
  • srandom(seed)方法
    • 为一个特定的对象实例设置随机数生成器的种子
    • 每次运行仿真，该对象产生的随机序列都将完全一致，便于复现失败的测试用例
1
2
3
4
5
6
7
8
9
class Generator;
    rand int data;
endclass

initial begin
    Generator g = new;
    g.srandom(100); // 将实例g的种子设置为100
    g.randomize();  // 每次仿真，只要种子是100，随机序列都相同
end
  • 仿真参数控制
    • VCS允许通过命令行参数指定全局种子：+ntb_random_seed=12345
    • 如果不手动指定种子，仿真器通常会使用系统时间作为默认种子，每次运行都会得到不同结果（类似手动指定+ntb_random_seed=$$(date +%N)的效果）

随机化函数

  • 对于SV随机化，除了使用CRT机制创建对象和定义约束，也可以直接调用仿真器内置的系统函数快速生成随机数，或在CRT中调用dist_*系列函数完成复杂随机化的建模

标准函数

  • random()：返回一个32位有符号的随机整数
  • urandom()：返回一个32位符号的随机整数
  • urandom_range(max,min)：返回一个指定范围内的无符号整数
    • 参数min的缺省值为0
    • 如果max比min小，参数列表会自动反向
1
2
3
4
5
6
7
int signed_var;
bit [31:0] unsigned_var;
int int_val;

signed_var = $random;           // 产生一个-2^18到2^18-1之间的随机整数，如 123456, -7854332
unsigned_var = $urandom;        // 产生一个0到2^32-1之间的随机整数，如 3489572349
int_val  = $urandom_range(100); // 生成一个 0 到 100 之间的数

分布函数

  • $dist_*系列概率分布函数，使用局部种子生成具有特定统计特性的随机序列
    • 用于模拟真实世界的噪声、延迟、故障间隔等场景
    • 都需要种子seed作为参数，控制随机序列
  • 由于SV CRT的约束块是声明式的，而随机化函数是一个过程化调用，故不能直接在约束块中使用随机化函数
    • 可以在约束块中使用概率约束中的dist关键词来近似模拟
    • 或者在回调函数 post_randomize()中调用dist_*系列函数进行后处理
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
// ==== 回调函数后处理 ==== //
class Packet;
    rand int delay; // 用于驱动的延迟值
    int delay_seed; // 专门用于delay分布的种子

    // 约束可以为空，或定义其他无关的约束
    constraint c_delay_basic {
        delay inside { [0:1000] }; // 可以提供一个基本的范围约束
    }

    // 在随机化后处理函数中生成分布
    function void post_randomize();
        real real_delay;
        real_delay = $dist_exponential(delay_seed, 50.0); // 生成均值为50的指数分布实数
        delay = int'(real_delay); // 将实数转换为整数，赋值给delay
    endfunction

    // 在new函数中初始化种子
    function new(int seed);
        delay_seed = seed;
    endfunction
endclass

initial begin
    Packet pkt = new(123); // 初始化种子
    pkt.randomize();       // 此时，pkt.delay 的值将是一个符合指数分布的整数
end

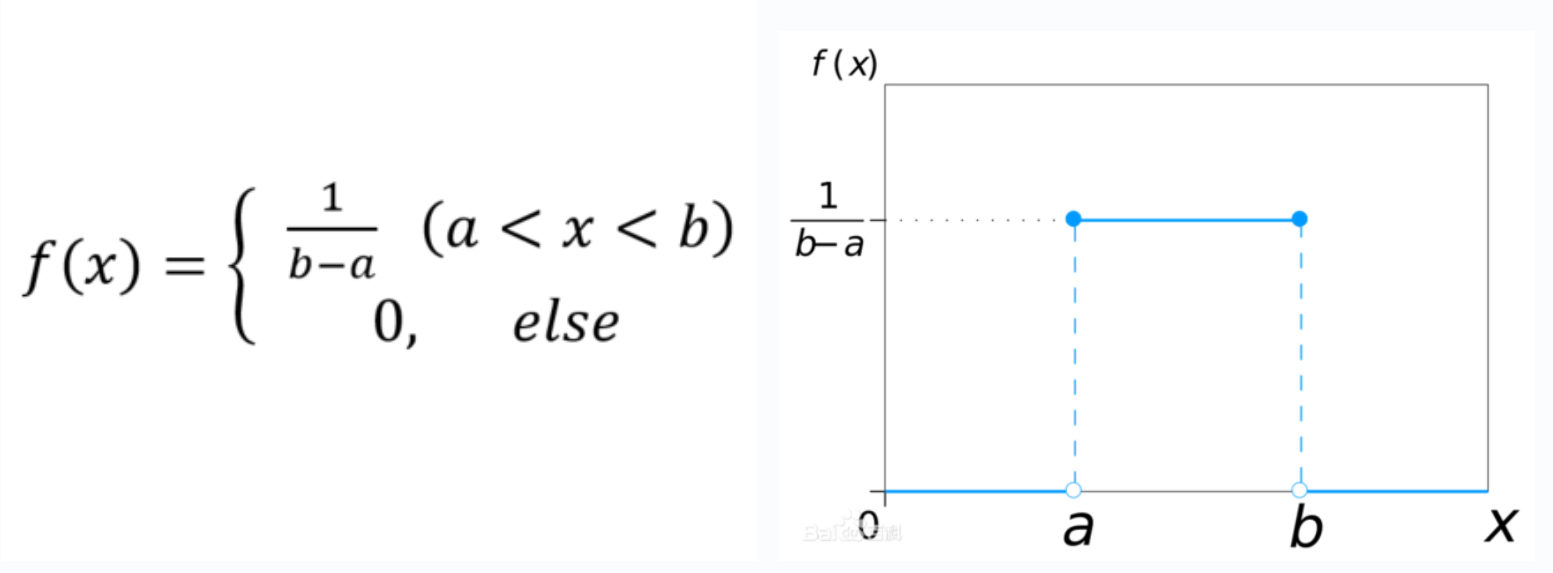
均匀分布

  • dist_uniform(seed, start, end)：以实数形式返回一个区间内的随机整数
    • start：范围起始整数
    • end：范围结束整数
image-20250827111723159 
1
2
3
4
// 模拟掷骰子
int seed = 123; // 初始化种子
int dice_roll;
dice_roll = $dist_uniform(seed, 1, 6); // 生成 1, 2, 3, 4, 5, 6 中的一个

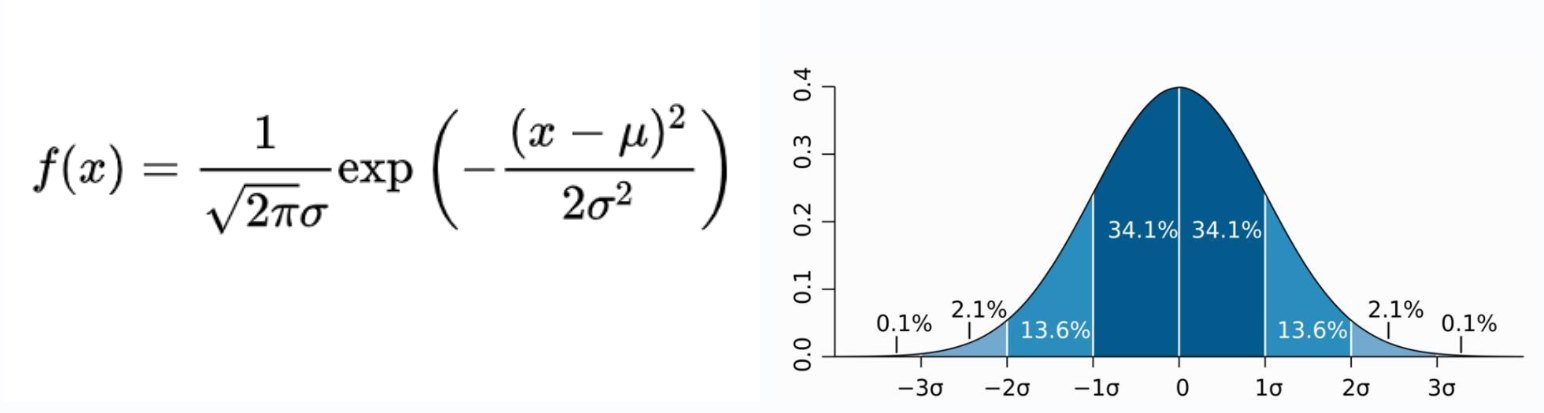
正态分布

  • dist_normal(seed, mean, std_dev)：经典“钟形分布”；返回一个符合正态分布的随机实数
    • mean：分布均值（期望值）
    • std_dev：分布标准差（大于0）
image-20250827111742532 
1
2
3
4
// 模拟一个期望值为 100ns，标准差为 15ns 的延迟
int seed = 456;
real delay;
delay = $dist_normal(seed, 100.0, 15.0); // 大部分delay值在85-115ns之间

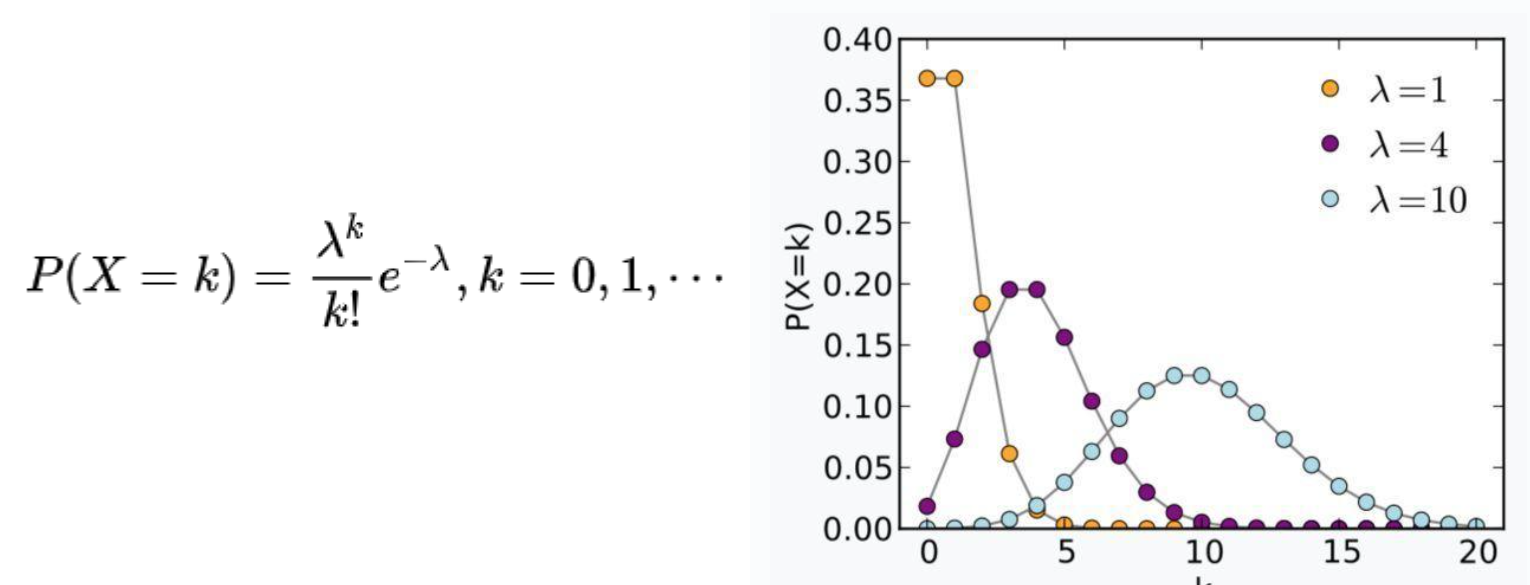
泊松分布

  • dist_poisson(seed, mean)：描述某个时间或空间范围内，某事件发生XX次的概率；以实数形式返回一个非负的随机整数
    • mean：期望，等于标准差
image-20250827113840916 
1
2
3
4
5
6
// 模拟一个小时内平均发生 3 次错误
real error_count_real;
int error_count;
int seed = 321;
error_count_real = $dist_poisson(seed, 3.0);
error_count = int'(error_count_real); // 转换为整型，如0, 1, 2, 3, ...

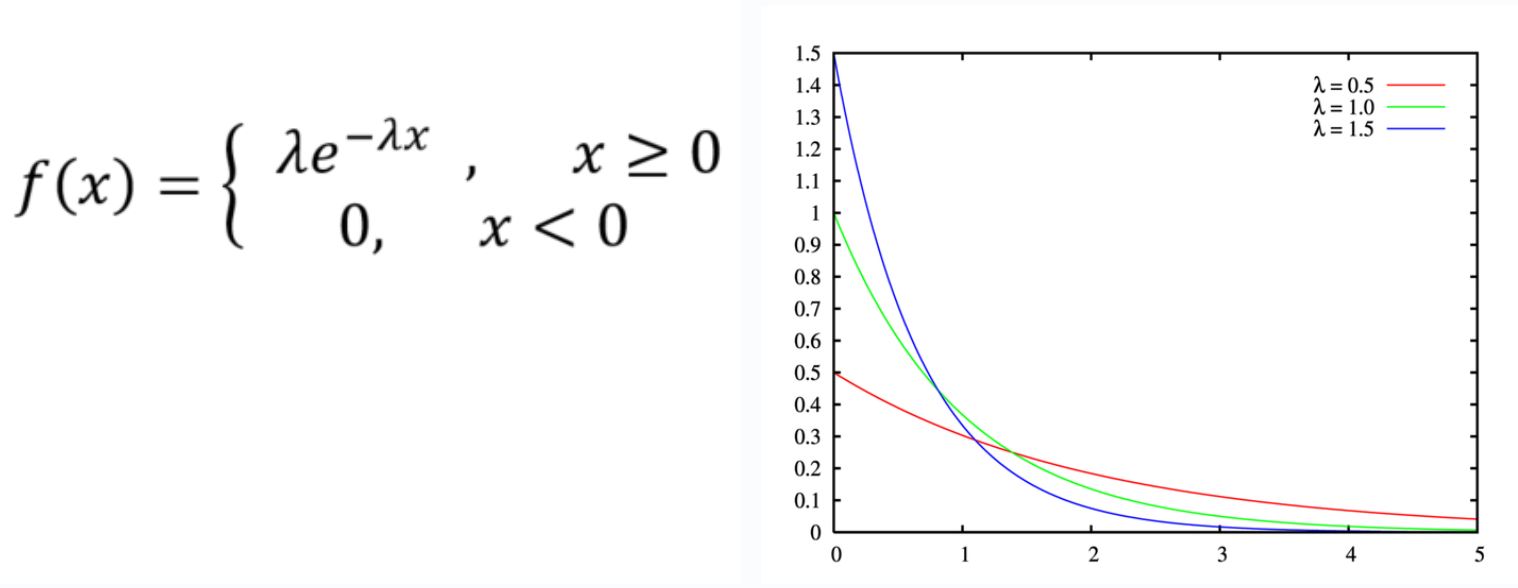
指数分布

  • dist_exponential(seed, mean)：描述泊松过程（即事件以恒定的平均速率连续且独立地发生的过程）中随机事件发生的时间间隔；返回一个非负的随机实数
    • mean：单位时间内，事件发生的次数
image-20250827113857767
  • 模拟平均每秒到达 5 个数据包的流量
1
2
3
int seed = 789;
real inter_arrival_time;
inter_arrival_time = $dist_exponential(seed, 1.0/5.0); // 平均间隔为0.2秒

卡方分布

  • dist_chi_square(seed, degree_of_freedom)：nn个服从标准正态分布的随机变量的平方和，构成新的随机变量的分布规律；返回一个非负的随机实数
    • degree_of_freedom：自由度nn，自由度越大，分布曲线越扁平，越接近正态分布
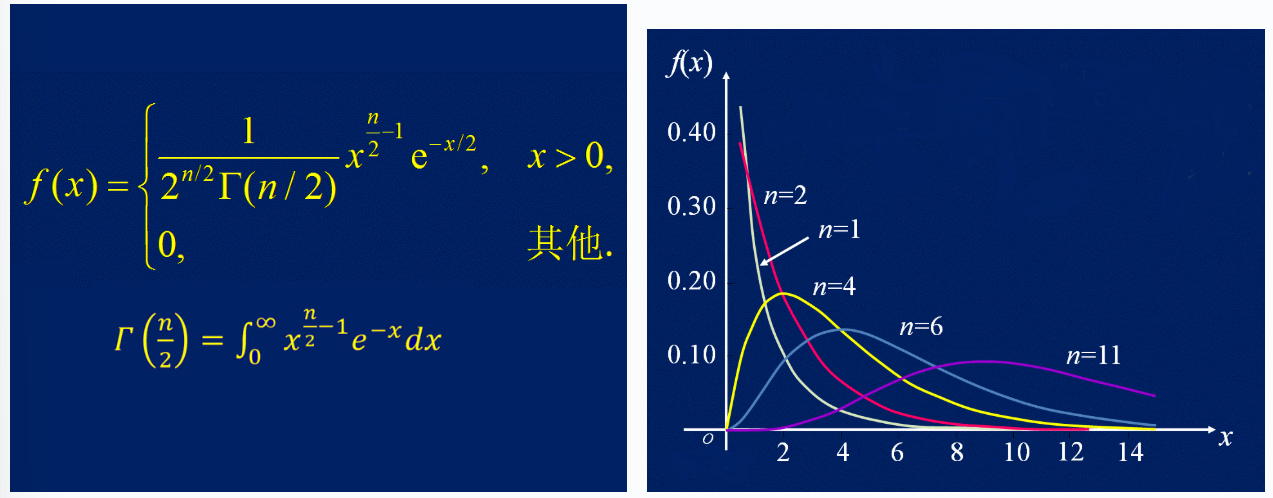
image-20250827161346569
  • 在验证中较少用于生成激励，更多用在测试平台分析组件或记分板进行统计检验
    • 下例是用卡方分布函数比较期望频数与实际观测频数之间的差异，如果根据这个统计量计算出的概率非常小，说明在原假设成立的前提下，观察到
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
// 假设检验一个随机数生成器（0-9）
int observed[10];
int seed = 123;
real chi_square_statistic = 0;
real expected_count;
real p_value_threshold = 0.05; // 显著性水平5%

// 生成大量随机数并统计，只考虑其中任意一个值如5时，只有是5与不是5两种情况，而根据中心极限定理，二项分布可以用正态分布近似，故后续可以统计这10个值的卡方分布
for (int i = 0; i < 10000; i++) begin
    int val = $urandom_range(9, 0);
    observed[val]++;
end

// 计算观测频数的卡方分布，卡方公式：Σ[(观测值 - 期望值)^2 / 期望值]
expected_count = 10000.0 / 10.0; // 每个数字期望出现1000次
foreach (observed[i]) begin
    chi_square_statistic += (observed[i] - expected_count) ** 2 / expected_count;
end

// 使用dist函数获取临界值，自由度为9，因为总频数已知，知道其中9个值得频率，剩下的那个频数也就清楚了
real critical_value = $dist_chi_square(seed, 9);

// 极度简化的判断逻辑，实际检验更复杂，用于检验这个随机假设是否符合要求
if (chi_square_statistic > critical_value) begin
    $display("WARNING: RNG may be biased! Chi-Square = %f", chi_square_statistic);
end else begin
    $display("RNG looks uniform. Chi-Square = %f", chi_square_statistic);
end

T分布

  • dist_t(seed, degree_of_freedom)：模拟出现极端值概率更高的随机现象；返回一个随机实数
    • degree_of_freedom：自由度
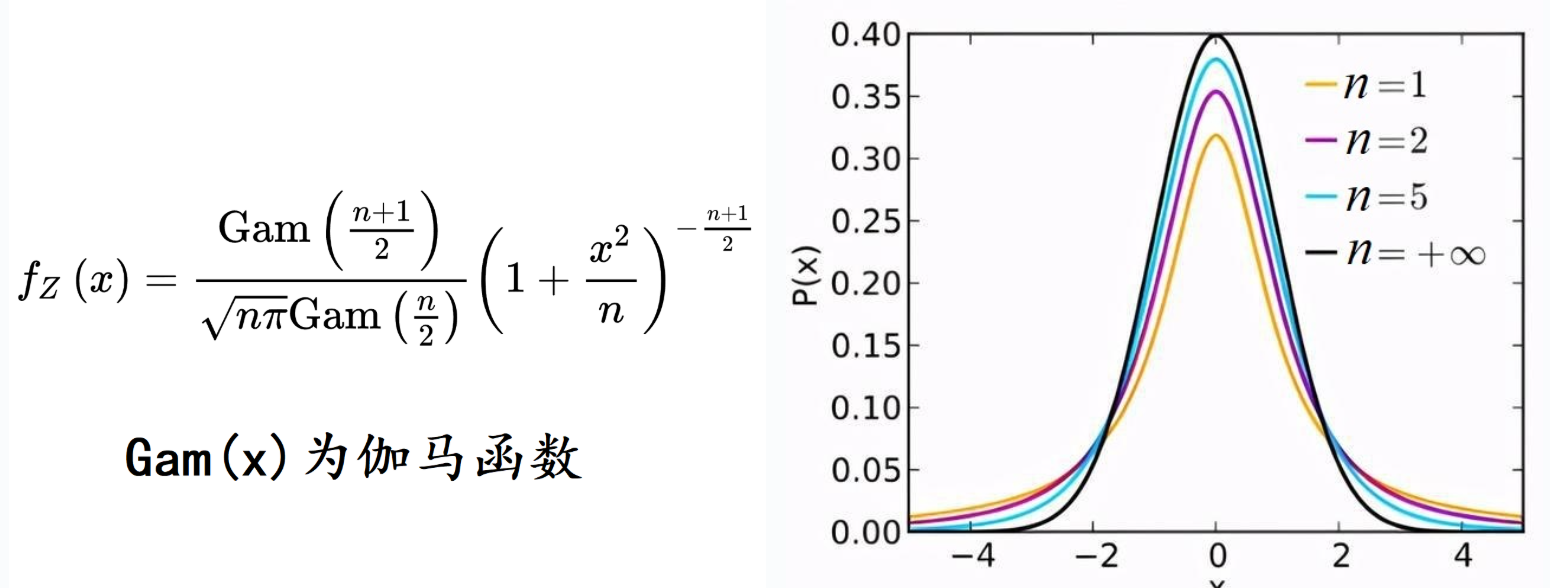
image-20250901141101463
  • 常用于对小样本或高方差过程进行建模，或模拟具有高不确定性的测量过程
    • 下例为模拟不稳定的传感器读数，$dist_t 生成的误差值出现 -4、+5 等极端值的概率，远高于 $dist_normal；这使得测试可以更容易地捕获到设计在处理异常输入时的潜在问题
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
module sensor_model;
    real nominal_voltage = 3.3; // 标称电压
    real measured_voltage;
    int t_seed = 200; // t分布专用种子
    real error_scale = 0.1; // 误差的缩放因子

    task read_voltage();
        real t_error;
        // 生成一个服从t分布（df=5）的随机误差
        t_error = $dist_t(t_seed, 5);
        // 将误差缩放后加到标称值上，得到测量值
        measured_voltage = nominal_voltage + (t_error * error_scale);
        $display("Measured Voltage: %f (Error: %f)", measured_voltage, t_error);
    endtask
endmodule

埃尔朗分布

  • dist_erlang(seed, k, mean)：指数分布的广义形式，描述的是kk次独立事件所需的总时间；返回一个非负的随机实数
    • k：形状参数（阶数，整数）
    • mean：分布的平均值
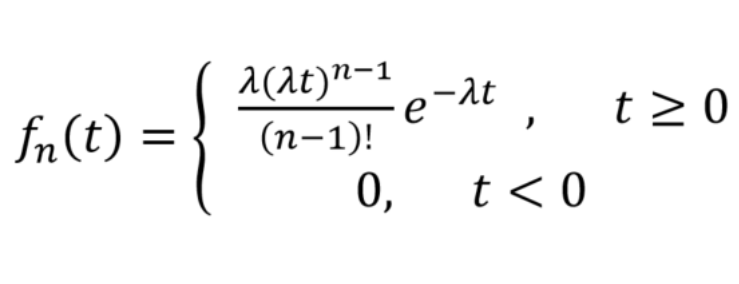
image-20250901141636517
  • 常用在通信和排队论中模拟总服务时间或总等待时间
    • 下例为模拟网络数据包的多级跳转传输延迟：假设一个数据包要依次经过 3 个网络节点（路由器）才能到达目的地；每个节点的处理延迟是随机的，且平均延迟为 1 个时间单位
1
2
3
4
5
6
7
8
9
10
11
class NetworkPacket;
    real total_delay; // 总延迟
    int erlang_seed = 300; // 埃尔朗分布专用种子
    constraint delay_range {
        // 总延迟的基本约束
    }
    function void post_randomize();
        // 生成总延迟：通过3个节点，平均总延迟为3.0个单位时间
        total_delay = $dist_erlang(erlang_seed, 3, 3.0);
    endfunction
endclass