LFSR原理
定义
- 线性反馈移位寄存器(Linear Feedback Shift Register,LFSR),其运算是确定的,所以,由寄存器所生成的数据流完全决定于寄存器当时或者之前的状态
- 种子:赋给 LFSR 的初始值
- 抽头:影响 LFSR 下一个状态的比特位
- 本源多项式:决定了线性移位寄存器的反馈结构
- 反馈系数 g_i 可以为0或1,但g_n和g_0只能为1
- 因为当 g_i 为0时表示不存在该反馈路径
- 逻辑运算:异或、同或
- 使用异或门的 LFSR 全
0状态下为无效状态 - 使用同或门的 LFSR 全
1状态下为无效状态 - 不管是异或还是同或,都需避免选择全
0或全1的种子,避免 LFSR 进入死循环
- 使用异或门的 LFSR 全
- 抽头序列:选取的某些位构成的序列
- 不同的抽头序列对应不同的本源多项式,产生不同的反馈路径
- 抽头的位置会影响LSFR的输出状态的最大长度序列(Maximum Length Sequence, MLS)
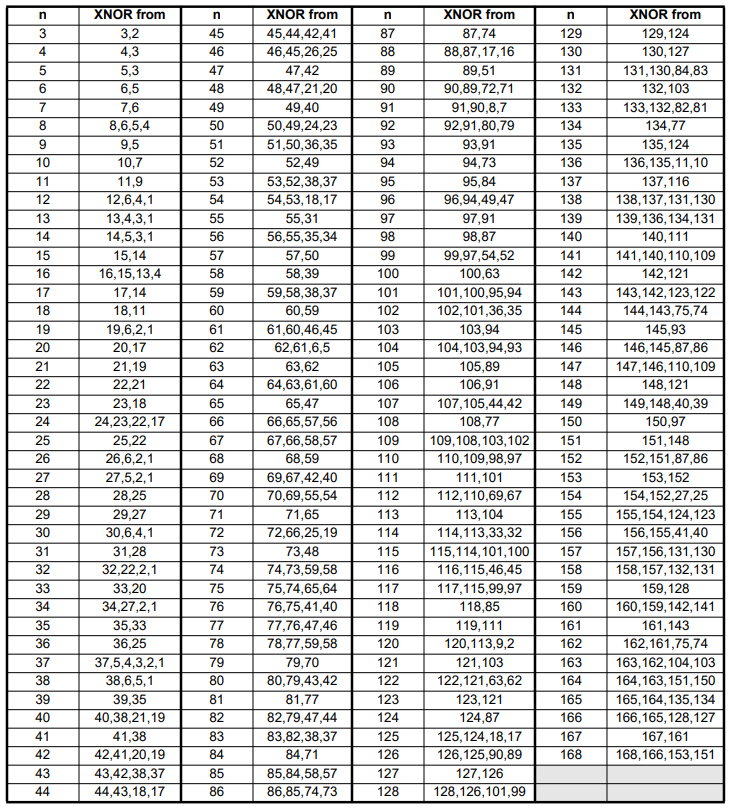
- 一个n bits的LFSR最多能输出种状态
- 能使LFSR拥有MLS的抽头序列不唯一
分类
外部型
- Fibonacci LFSR:斐波那契(外部 LFSR),又称 many-to-one
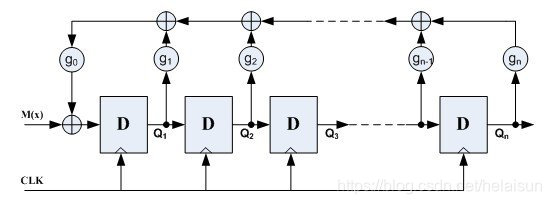
- 下例是一个本源多项式为的 Fibonacci LFSR
- 抽头序列是
[16,14,13,11] - 抽头依次与输出比特进行异或运算,然后反馈回最左端的位
- LFSR 最右端的比特为输出比特,当前状态为
0x8735,下一个状态是0x0E6A
- 抽头序列是
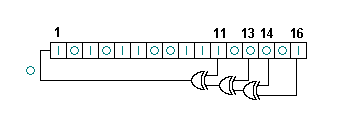
内部型
- Galois LFSR:伽罗瓦(内部LFSR),又称one-to-many
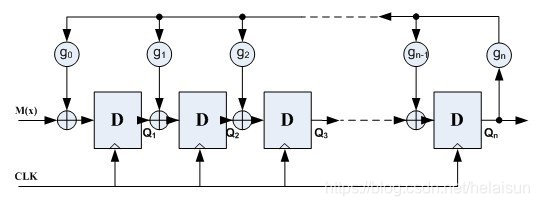
- 下例是一个本源多项式为的 Galois LFSR
- 抽头序列为
[3,2]
- 抽头序列为
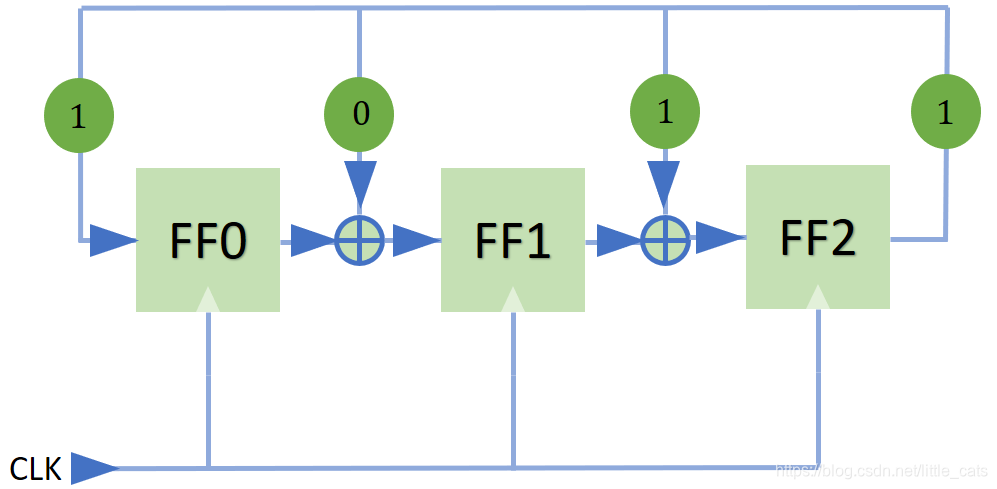
- 这个3位的LFSR的伪功能代码可以用C描述为
1 | void lfsr3() |
- 从上述代码的状态转移图中可以发现7个状态组成一个循环,这也是3为LFSR所能达到的最多状态
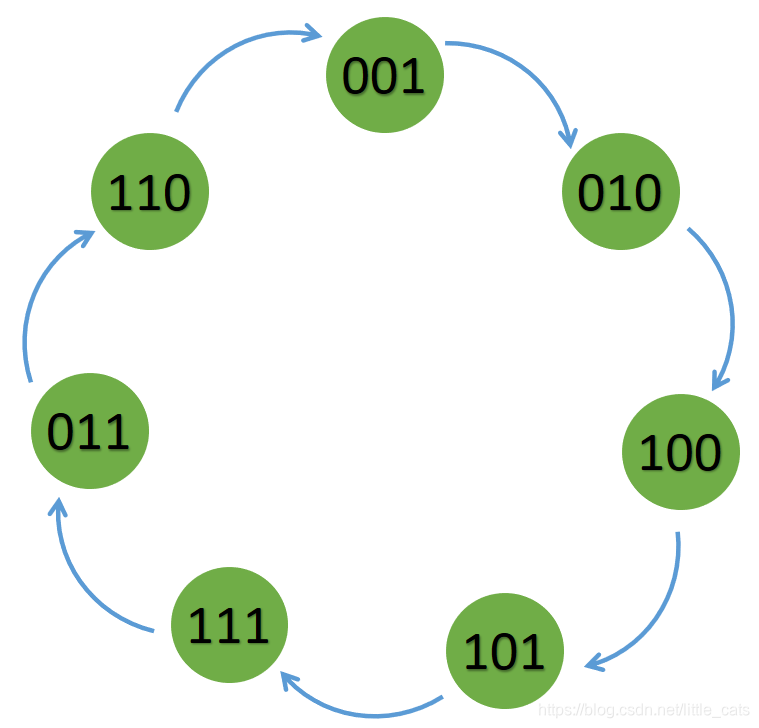
实例
- 抽头序列为
[3,2]的3级Fibonacci LFSR
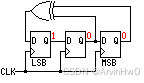
1 | module Fibonacci_LFSR3_D( |
- 抽头序列为
[4,2]的4级Fibonacci LFSR
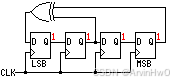
1 | module Fibonacci_LFSR4_15( |
- 抽头序列为
[4,1]的4级Fibonacci LFSR
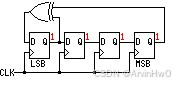
1 | module Fibonacci_LFSR4_13( |
- 抽头序列为
[16,14,13,11]的16级Fibonacci LFSR

1 | module Fibonacci_LFSR16_16801( |
- 若需要将全0状态加入上述LFSR的循环中

1 | module Fibonacci_LFSR16_16801_0( |
应用
- 伪随机数生成
- LFSR只能产生伪随机,是伪随机数生成器(Pseudo Random Number Generator,PRNG)的一种实现方案,在实际应用中,可以使用一些分立器件如D触发器构造LFSR
- 虽然在反馈路径确定后,LFSR的输出状态序列也是确定的,且最终会实现循环,但随着n的增大,任意时刻的输出状态的随机性也会随之增大
- 数据加密
- 数据发送端通过加扰将源数据流与一个随机序列异或后,再发送出去,异或操作完成后的数据流基本是伪随机的
- 在数据接收端也有解扰操作,解扰与加扰必须完全同步,即LFSR使用相同的公式、相同的初始值、相同时刻的输出
- CRC校验
- LFSR还可用于CRC的校验,会用到模2的多项式运算,遵循如下的运算原则:
